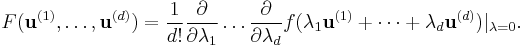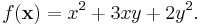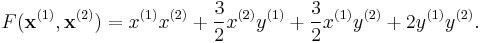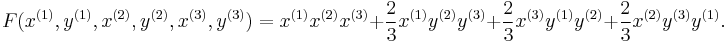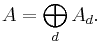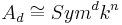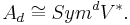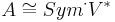Polarization of an algebraic form

In mathematics, in particular in algebra, polarization is a technique for expressing a homogeneous polynomial in a simpler fashion by adjoining more variables. Specifically, given a homogeneous polynomial, polarization produces a multilinear form from which the original polynomial can be recovered by evaluating along a certain diagonal.

Although the technique is deceptively simple, it has applications in many areas of abstract mathematics: in particular to algebraic geometry, invariant theory, and representation theory. Polarization and related techniques form the foundations for Weyl's invariant theory.

1 The technique
2 Examples
3 Mathematical details and consequences

The technique

The fundamental ideas are as follows. Let f(u) be a polynomial in n variables u = (u₁, u₂, ..., u_n). Suppose that f is homogeneous of degree d, which means that

f(t u) = t^d f(u) for all t.

Let u⁽¹⁾, u⁽²⁾, ..., u^(d) be a collection of indeterminates with u⁽ⁱ⁾ = (u₁⁽ⁱ⁾, u₂⁽ⁱ⁾, ..., u_n⁽ⁱ⁾), so that there are dn variables altogether. The polar form of f is a polynomial

F(u⁽¹⁾, u⁽²⁾, ..., u^(d))

which is linear separately in each u⁽ⁱ⁾ (i.e., F is multilinear), symmetric in the u⁽ⁱ⁾, and such that

F(u,u, ..., u)=f(u).

The polar form of f is given by the following construction

$F({\bold u}^{(1)},\dots,{\bold u}^{(d)})=\frac{1}{d!}\frac{\partial}{\partial\lambda_1}\dots\frac{\partial}{\partial\lambda_d}f(\lambda_1{\bold u}^{(1)}%2B\dots%2B\lambda_d{\bold u}^{(d)})|_{\lambda=0}.$

In other words, F is a constant multiple of the coefficient of λ₁ λ₂...λ_d in the expansion of f(λ₁u⁽¹⁾ + ... + λ_du^(d)).

Examples

Suppose that x=(x,y) and f(x) is the quadratic form

$f({\bold x}) = x^2 %2B 3 x y %2B 2 y^2.$

Then the polarization of f is a function in x⁽¹⁾ = (x⁽¹⁾, y⁽¹⁾) and x⁽²⁾ = (x⁽²⁾, y⁽²⁾) given by

$F({\bold x}^{(1)},{\bold x}^{(2)}) = x^{(1)}x^{(2)}%2B\frac{3}{2}x^{(2)}y^{(1)}%2B\frac{3}{2}x^{(1)}y^{(2)}%2B2 y^{(1)}y^{(2)}.$

More generally, if f is any quadratic form, then the polarization of f agrees with the conclusion of the polarization identity.

A cubic example. Let f(x,y)=x³ + 2xy². Then the polarization of f is given by

$F(x^{(1)},y^{(1)},x^{(2)},y^{(2)},x^{(3)},y^{(3)})= x^{(1)}x^{(2)}x^{(3)}%2B\frac{2}{3}x^{(1)}y^{(2)}y^{(3)}%2B\frac{2}{3}x^{(3)}y^{(1)}y^{(2)}%2B\frac{2}{3}x^{(2)}y^{(3)}y^{(1)}.$

Mathematical details and consequences

The polarization of a homogeneous polynomial of degree d is valid over any commutative ring in which d! is a unit. In particular, it holds over any field of characteristic zero or whose characteristic is strictly greater than d.

The polarization isomorphism (by degree)

For simplicity, let k be a field of characteristic zero and let A=k[x] be the polynomial ring in n variables over k. Then A is graded by degree, so that

$A = \bigoplus_d A_d.$

The polarization of algebraic forms then induces an isomorphism of vector spaces in each degree

$A_d \cong Sym^d k^n$

where Sym^d is the d-th symmetric power of the n-dimensional space kⁿ.

These isomorphisms can be expressed independently of a basis as follows. If V is a finite-dimensional vector space and A is the ring of k-valued polynomial functions on V, graded by homogeneous degree, then polarization yields an isomorphism

$A_d \cong Sym^d V^*.$

The algebraic isomorphism

Furthermore, the polarization is compatible with the algebraic structure on A, so that

$A \cong Sym^\cdot V^*$

where Sym^.V^* is the full symmetric algebra over V^*.

Remarks

For fields of positive characteristic p, the foregoing isomorphisms apply if the graded algebras are truncated at degree p-1.
There do exist generalizations when V is an infinite dimensional topological vector space.